Home => ProblemSet => 101.2024-04:永恒(Eternity)
2157: 101.2024-04:永恒(Eternity)
Time Limit: 4 Sec Memory Limit: 512 MB Submit: 0 Solved: 1[ Submit ] [ Status ] [ Creator: ][ 参考程序 ]
Description
一些前置定义:
问有多少不同的大小为 n 的可重集 S 满足:
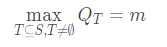
其中 QT 为可重集 T 的权值。
注意:根据可重集的性质,数字相同但数字顺序不同的可重集算同一种可重集,即 {1,2,3} 与 {3,2,1} 算同一种可重集。
求出不同可重集的个数 mod 998244353 的结果。
可以证明这样的可重集个数是有限的。
-
可重集中的元素必须是非负整数。
-
可重集的大小为可重集中元素的个数。
-
对于一个大小为 x 的可重集,设其中的元素为 a1,a2…ax,那么这个可重集的权值就为 a1⊕a2⊕⋯⊕ax,即可重集中所有元素的异或和。
问有多少不同的大小为 n 的可重集 S 满足:
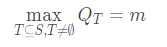
其中 QT 为可重集 T 的权值。
注意:根据可重集的性质,数字相同但数字顺序不同的可重集算同一种可重集,即 {1,2,3} 与 {3,2,1} 算同一种可重集。
求出不同可重集的个数 mod 998244353 的结果。
可以证明这样的可重集个数是有限的。
Input
第一行两个整数,分别表示 n 和 m。
Output
一行一个整数,表示答案对 998244353 取模后的结果。
Sample Input Copy
3 5
Sample Output Copy
13
HINT
样例二:
输入:
12 7
输出:
48643
(0,0,5),(0,1,4),(0,1,5),(0,4,5),(0,5,5),(1,1,4),(1,1,5),(1,4,4),(1,4,5),(1,5,5),(4,4,5),(4,5,5),(5,5,5)。
输入:
12 7
输出:
48643
【样例解释】
样例一中 13 种方案分别为:(0,0,5),(0,1,4),(0,1,5),(0,4,5),(0,5,5),(1,1,4),(1,1,5),(1,4,4),(1,4,5),(1,5,5),(4,4,5),(4,5,5),(5,5,5)。
