Home => ProblemSet => 2.12-111:「Stoi2031」蒲公英的约定(vol.1)
2110: 2.12-111:「Stoi2031」蒲公英的约定(vol.1)
Time Limit: 1 Sec Memory Limit: 128 MB Submit: 0 Solved: 0[ Submit ] [ Status ] [ Creator: ][ 参考程序 ]
Description
清和如在玩游戏。她们有 n 丛 蒲公英,每丛分别有 si 朵。这些 蒲公英 有一个神奇的性质:有一个给定的常数 σ∈(0,1),x 朵 蒲公英 会分出 ⌊σx⌋ 朵为一组,剩下x−⌊σx⌋ 朵继续分组,直到分出的组没有 蒲公英 即 ⌊σx⌋=0 为止。
她们称这种现象为 任性。现在她们的每丛 蒲公英 都有 任性 的现象。她们的游戏规则如下:从清开始,两人轮流进行 旅行。一次 旅行 为选择一丛 蒲公英 并吹散这一丛的第一组中的若干朵 蒲公英,至少要吹一朵,至多吹的朵数为第一组的朵数,即不能吹散除第一组外的 蒲公英。
当第一组为空时,其下一组成为第一组。若这一丛只剩下一组 蒲公英,这一丛不能再被选定。每丛 蒲公英 都不能被选定时,游戏结束,当前轮到的人落败。
她们想知道如果清第一次 旅行 时等概率选择其中一丛可吹散的 蒲公英 再等概率选择吹散的朵数后两人都按最优策略操作,那么清的胜率 x mod 20190816170251 的值将会是多少。
与 vol.2 的区别是,蒲公英 在被吹散一部分后 不会 重新分组。
Input
第一行两个正整数 id,n,其中 id 表示 Subtask 编号。
第二行 n 个正整数,第 i 个表示 si。
若 id>3,第三行输入两个正整数 p,q 表示 σ=q / p。
Output
一行一个整数,表示清的胜率 x mod 20190816170251。
Sample Input Copy
4 3
1 1 1
1 6
Sample Output Copy
0
HINT
样例二:
输入:
6 3
1 7 3
1 3
输出:
5047704042563

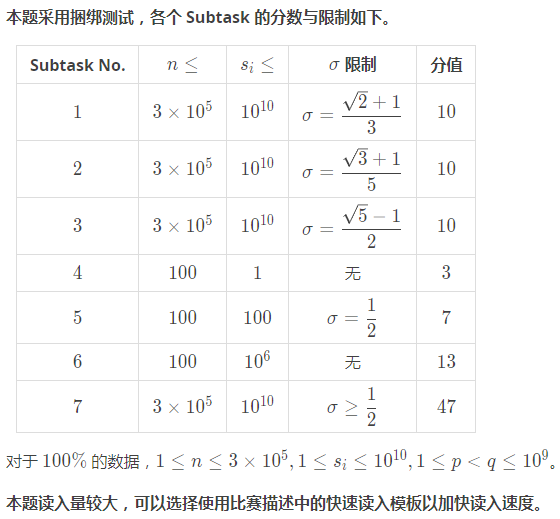
输入:
6 3
1 7 3
1 3
输出:
5047704042563

