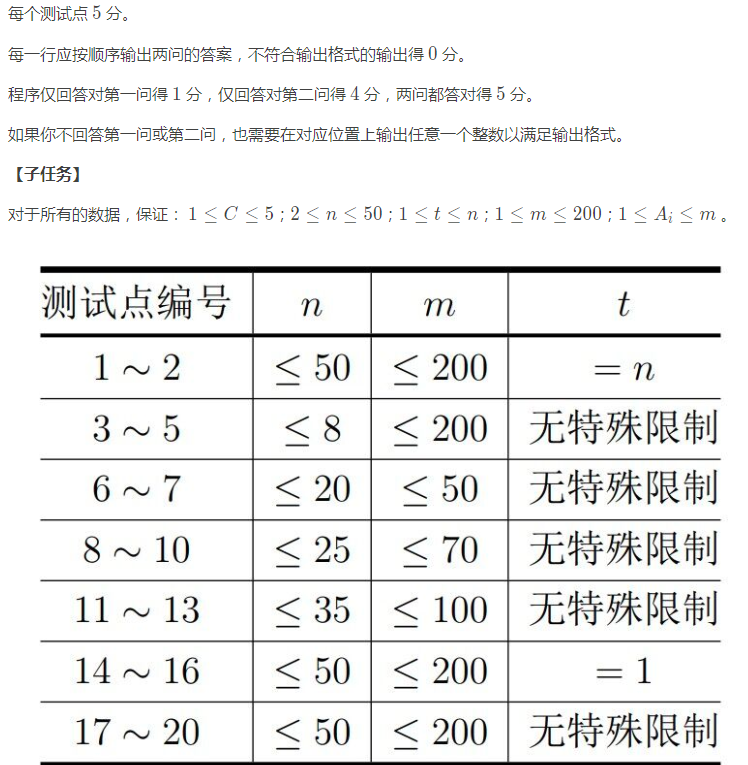
Home => ProblemSet => 100.2023-06:染色数组
1984: 100.2023-06:染色数组
Time Limit: 3 Sec Memory Limit: 1024 MB Submit: 0 Solved: 0[ Submit ] [ Status ] [ Creator: ][ 参考程序 ]
Description
给定一个长度为 n 的正整数数组 A,其中每个数都在 1 到 m 之间,从左到右排成一排。现在要将每个数字染成红色或者绿色,我们定义一个染色方案为优秀的染色方案,当且仅当它满足:
如果一个数组至少存在两个不同的优秀的染色方案,那么称这个数组是完美的。(两个染色方案不同当且仅当至少存在一个位置上的数字被染成不同的颜色)。
例如,193476 和 1955 都是完美的,因为上面已经分别给出了 2 种优秀的染色方案。而 2333 则不是完美的,因为找不到任何一种优秀的染色方案。同时 15364 也不是完美的,因为仅存在一种优秀的染色方案(15364)。
补充说明:如果红色的数只有 0 个或者 1 个,我们也认为它严格递增;同理如果绿色的数只有 0 个或者 1 个,我们也认为它严格递减。例如 123,123 都是优秀的的染色方案,因此 123 是完美的数组。
我们定义一种给染色方案打分的方式。
对于每个的有序元素对 Ai,Aj(i<j) :
一个完美的数组的得分为它所有优秀的染色方案的得分的最大值。
现在确定数组 A 的前 t 个数 A1,A2,…,At, 你需要回答以下两个问题:
- 每个数 Ai 要么被染成红色,要么被染成绿色。
- 红色的数从左到右依次严格递增,绿色的数从左到右依次严格递减。
如果一个数组至少存在两个不同的优秀的染色方案,那么称这个数组是完美的。(两个染色方案不同当且仅当至少存在一个位置上的数字被染成不同的颜色)。
例如,193476 和 1955 都是完美的,因为上面已经分别给出了 2 种优秀的染色方案。而 2333 则不是完美的,因为找不到任何一种优秀的染色方案。同时 15364 也不是完美的,因为仅存在一种优秀的染色方案(15364)。
补充说明:如果红色的数只有 0 个或者 1 个,我们也认为它严格递增;同理如果绿色的数只有 0 个或者 1 个,我们也认为它严格递减。例如 123,123 都是优秀的的染色方案,因此 123 是完美的数组。
我们定义一种给染色方案打分的方式。
对于每个的有序元素对 Ai,Aj(i<j) :
- 如果 Aj 染成红色,且 Aj<Ai,则该元素对得 m−Aj+1 分;
- 如果 Aj 染成绿色,且 Aj>Ai,则该元素对得 Aj 分;
- 不满足 1 或 2 ,则该元素对得 0 分。
一个完美的数组的得分为它所有优秀的染色方案的得分的最大值。
现在确定数组 A 的前 t 个数 A1,A2,…,At, 你需要回答以下两个问题:
- 第一问:有多少种确定 A 中后 n−t 个数的方案使得 A 是一个完美数组?
- 第二问:所有可能的完美数组的得分和是多少?
Input
本题有多组测试数据。
输入的第一行包含一个正整数 C,表示数据组数。
接下来包含 C 组数据,每组数据的格式如下:
第一行包含三个整数 n,m,t,分别表示数组长度,数组内数字的最大值和确定的前缀长度。
第二行包含 t 个正整数 A1…At,表示已经确定的前缀。
输入的第一行包含一个正整数 C,表示数据组数。
接下来包含 C 组数据,每组数据的格式如下:
第一行包含三个整数 n,m,t,分别表示数组长度,数组内数字的最大值和确定的前缀长度。
第二行包含 t 个正整数 A1…At,表示已经确定的前缀。
Output
对于每组测试数据输出一行包含两个用单个空格隔开的整数。
-
第一个整数表示优秀数组的数量模 998244353 的值;
-
第二个整数表示优秀数组的得分之和模 998244353 的值。
Sample Input Copy
5
6 10 6
1 9 3 4 7 6
5 8 4
1 7 2 6
9 10 2
3 6
6 11 6
1 7 5 8 3 9
9 10 5
5 10 6 4 7
Sample Output Copy
1 63
8 245
29378 1267731
1 17
78 1820