Home => ProblemSet => 3.13-02:重链剖分/树链剖分
1860: 3.13-02:重链剖分/树链剖分
Time Limit: 1 Sec Memory Limit: 128 MB Submit: 0 Solved: 2[ Submit ] [ Status ] [ Creator: ][ 参考程序 ]
Description
如题,已知一棵包含 N 个结点的树(连通且无环),每个节点上包含一个数值,需要支持以下操作:
-
1 x y z,表示将树从 x 到 y 结点最短路径上所有节点的值都加上 z。
-
2 x y,表示求树从 x 到 y 结点最短路径上所有节点的值之和。
-
3 x z,表示将以 x 为根节点的子树内所有节点值都加上 z。
-
4 x 表示求以 x 为根节点的子树内所有节点值之和
Input
第一行包含 4 个正整数 N,M,R,P,分别表示树的结点个数、操作个数、根节点序号和取模数(即所有的输出结果均对此取模)。
接下来一行包含 N 个非负整数,分别依次表示各个节点上初始的数值。
接下来 N−1 行每行包含两个整数 x,y,表示点 x 和点 y 之间连有一条边(保证无环且连通)。
接下来 M 行每行包含若干个正整数,每行表示一个操作。
接下来一行包含 N 个非负整数,分别依次表示各个节点上初始的数值。
接下来 N−1 行每行包含两个整数 x,y,表示点 x 和点 y 之间连有一条边(保证无环且连通)。
接下来 M 行每行包含若干个正整数,每行表示一个操作。
Output
输出包含若干行,分别依次表示每个操作 2 或操作 4 所得的结果(对 P 取模)。
Sample Input Copy
5 5 2 24
7 3 7 8 0
1 2
1 5
3 1
4 1
3 4 2
3 2 2
4 5
1 5 1 3
2 1 3
Sample Output Copy
2
21
HINT
样例说明:
树的结构
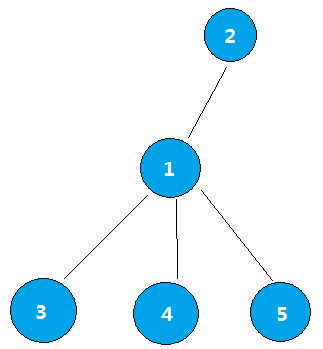
各个操作如下:
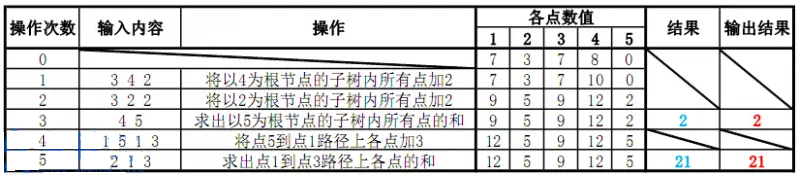
结果为2 和 21
对于 30% 的数据: 1≤N≤10, 1≤M≤10;
对于 70% 的数据: 1≤N≤103, 1≤M≤103;
对于 100% 的数据: 1≤N≤105, 1≤M≤105, 1≤R≤N, 1≤P≤231−1。
树的结构

各个操作如下:

结果为2 和 21
对于 30% 的数据: 1≤N≤10, 1≤M≤10;
对于 70% 的数据: 1≤N≤103, 1≤M≤103;
对于 100% 的数据: 1≤N≤105, 1≤M≤105, 1≤R≤N, 1≤P≤231−1。