Byteasar the gardener is growing a rare tree called Rotatus Informatikus. It has some interesting features: The tree consists of straight branches, bifurcations and leaves. The trunk stemming from the ground is also a branch. Each branch ends with either a bifurcation or a leaf on its top end. Exactly two branches fork out from a bifurcation at the end of a branch - the left branch and the right branch. Each leaf of the tree is labelled with an integer from the range . The labels of leaves are unique. With some gardening work, a so called rotation can be performed on any bifurcation, swapping the left and right branches that fork out of it. The corona of the tree is the sequence of integers obtained by reading the leaves' labels from left to right. Byteasar is from the old town of Byteburg and, like all true Byteburgers, praises neatness and order. He wonders how neat can his tree become thanks to appropriate rotations. The neatness of a tree is measured by the number of inversions in its corona, i.e. the number of pairs（I,j）, (1< = I < j < = N ) such that(Ai>Aj) in the corona(A1,A2,A3…An).  
The original tree (on the left) with corona(3,1,2) has two inversions. A single rotation gives a tree (on the right) with corona(1,3,2), which has only one inversion. Each of these two trees has 5 branches. Write a program that determines the minimum number of inversions in the corona of Byteasar's tree that can be obtained by rotations.
给定一颗有 n 个叶节点的二叉树。每个叶节点都有一个权值 pi（注意，根不是叶节点），所有叶节点的权值构成了一个 1∼n 的排列。
对于这棵二叉树的任何一个结点，保证其要么是叶节点，要么左右两个孩子都存在。
现在你可以任选一些节点，交换这些节点的左右子树。
在最终的树上，按照先序遍历遍历整棵树并依次写下遇到的叶结点的权值构成一个长度为 n 的排列，你需要最小化这个排列的逆序对数。

In the first line of the standard input there is a single integer (2< = N < = 200000) that denotes the number of leaves in Byteasar's tree. 
Next, the description of the tree follows. 
The tree is defined recursively:
if there is a leaf labelled with (1<=P<=N) at the end of the trunk (i.e., the branch from which the tree stems), then the tree's description consists of a single line containing a single integer;
if there is a bifurcation at the end of the trunk, then the tree's description consists of three parts: the first line holds a single number , then the description of the left subtree follows (as if the left branch forking out of the bifurcation was its trunk), and finally the description of the right subtree follows (as if the right branch forking out of the bifurcation was its trunk).
第一行是一个整数 n，表示树的叶节点个数。
接下来若干行，使用递归的形式来读入这棵树，读入任意一个子树的信息时，初始时读入其根节点。对于一个结点 u，首先有一行一个整数 x。

• 若 x != 0，则表示 u 是一个叶节点，其权值为 x。
• 若 x=0，则表示 u 不是叶节点，则接下来若干行读入其左子树信息，左子树读入结束后接下来若干行读入其右子树信息。

In the first and only line of the standard output a single integer is to be printed: the minimum number of inversions in the corona of the input tree that can be obtained by a sequence of rotations.

一行，最少逆序对个数

样例解释：
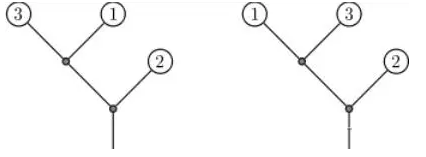
下图中，左图是初始读入的树，右图是操作后的树。

• 对于 $30\%$ 的数据，保证 n≤5×10³。
• 对于 $100\%$ 的数据，保证 2≤n≤2×10⁵， $0\le x\le n$，所有叶节点的权值是一个 $1\sim n$ 的排列。

P3521 数据结构 线段树 树状数组