Home => ProblemSet => 5.1-08:矩阵编码
1291: 5.1-08:矩阵编码
Time Limit: 1 Sec Memory Limit: 128 MB Submit: 0 Solved: 0[ Submit ] [ Status ] [ Creator: ][ 参考程序 ]
Description
有一个变长为 N(N=2n) 的正方形矩阵,其中元素均为0或1,如下方左图所示。
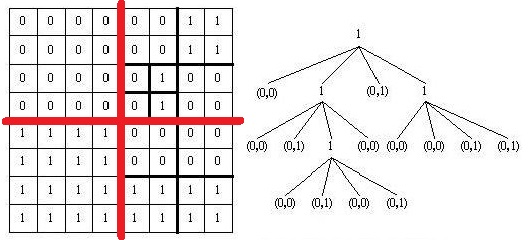
为了保存左图这样的矩阵,经常使用四分树来完成。对于一个 N∗N 的矩阵,N≤512 且 N=2i,如果这个矩阵中的数不全一样,那么我们会把这个矩阵分成4个 N/2∗N/2 的矩阵,如左图中红色粗线所示。
之后,我们再对这4个 N/2∗N/2 的矩阵进行划分,同样地,如果里面的数不全一样则划分成 N/4∗N/4 的矩阵。左图里面右边的两个 N/2∗N/2 的矩阵就被这样再度划分了。如此可以持续进行划分,直到里面的数全一样。左图粗线展示了完全划分完毕的样子。
我们一般都将矩阵存成右图这样的四分数的形式,这棵树是通过左图里面的划分得到的。右图里面的每一个节点都代表左图里面的矩阵,而树的根结点代表整个大的矩阵。如果树中一个结点的值为1,则代表这个结点对应的矩阵需要划分成4个小矩阵(对应的4个节点按照左上、右上、左下、右下的顺序进行排列,可参考题目配图)。否则,这个结点将包含两个数。第一个数为0,表示不用再划分,第二个数为0,表示整个矩阵都是这个值。整棵树可以用它的宽度优先遍历得到的结果来表示,如右图的树可以表示为
(1)(0,0)(1)(0,1)(1)(0,0)(0,1)(1)(0,0)(0,0)(0,0)(0,1)(0,1)(0,0)(0,1)(0,0)(0,1)
删掉括号和逗号,我们可以得到一个更简短的纯二进制编码:
100101100011000000010100010001
现在请你编写一个程序,求出给定矩阵的二进制形式的编码。

为了保存左图这样的矩阵,经常使用四分树来完成。对于一个 N∗N 的矩阵,N≤512 且 N=2i,如果这个矩阵中的数不全一样,那么我们会把这个矩阵分成4个 N/2∗N/2 的矩阵,如左图中红色粗线所示。
之后,我们再对这4个 N/2∗N/2 的矩阵进行划分,同样地,如果里面的数不全一样则划分成 N/4∗N/4 的矩阵。左图里面右边的两个 N/2∗N/2 的矩阵就被这样再度划分了。如此可以持续进行划分,直到里面的数全一样。左图粗线展示了完全划分完毕的样子。
我们一般都将矩阵存成右图这样的四分数的形式,这棵树是通过左图里面的划分得到的。右图里面的每一个节点都代表左图里面的矩阵,而树的根结点代表整个大的矩阵。如果树中一个结点的值为1,则代表这个结点对应的矩阵需要划分成4个小矩阵(对应的4个节点按照左上、右上、左下、右下的顺序进行排列,可参考题目配图)。否则,这个结点将包含两个数。第一个数为0,表示不用再划分,第二个数为0,表示整个矩阵都是这个值。整棵树可以用它的宽度优先遍历得到的结果来表示,如右图的树可以表示为
(1)(0,0)(1)(0,1)(1)(0,0)(0,1)(1)(0,0)(0,0)(0,0)(0,1)(0,1)(0,0)(0,1)(0,0)(0,1)
删掉括号和逗号,我们可以得到一个更简短的纯二进制编码:
100101100011000000010100010001
现在请你编写一个程序,求出给定矩阵的二进制形式的编码。
Input
第一行一个正整数 T,表示数据组数。
每组数据第一行一个正整数 N,表示矩阵的大小,保证存在正整数 n,使得 N=2n,接下来是一个 N∗N 的待编码的01矩阵,同一行相邻两个数之间有空格隔开。
每组数据第一行一个正整数 N,表示矩阵的大小,保证存在正整数 n,使得 N=2n,接下来是一个 N∗N 的待编码的01矩阵,同一行相邻两个数之间有空格隔开。
Output
对每组数据输出一行,表示该图片的二进制编码。
Sample Input Copy
2
2
0 0
0 0
4
0 0 1 1
0 0 1 1
1 1 0 0
1 1 0 0
Sample Output Copy
00
100010100
HINT
对于 50% 的数据,1≤T≤10,2≤N≤64。
对于 100% 的数据,1≤T≤50,2≤N≤512,每个测试点中 N≥128 的数据不超过3组。
数据规模较大,请使用 cstdio 中的 scanf 和 printf 函数进行输入输出。
对于 100% 的数据,1≤T≤50,2≤N≤512,每个测试点中 N≥128 的数据不超过3组。
数据规模较大,请使用 cstdio 中的 scanf 和 printf 函数进行输入输出。